درخت جستجوی دودویی (BST)؛ یک درخت جستجوی مرتب

مجموعه: متفرقه اينترنت و كامپيوتر

الگوریتم درخت جستجوی دودویی

درخت جستجوی دودویی: ساختار داده ای کارآمد برای جستجوی داده ها 

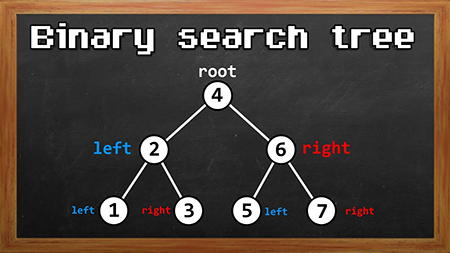
درخت جستجوی دودویی (BST) یک ساختار داده است که برای ذخیره و بازیابی داده‌ها استفاده می‌شود. BST ها به طور مرتب ، مرتب می‌شوند، به این معنی که هر عنصر در BST بزرگتر از همه عناصر در سمت چپ آن و کوچکتر از همه عناصر در سمت راست آن است. این ویژگی درخت جستجوی دودویی را به یک ساختار داده بسیار کارآمد برای جستجوی داده‌ها تبدیل می‌کند.

برای جستجوی یک عنصر معین، از گره ریشه شروع می کنیم و کلید عنصر را با کلید گره ریشه مقایسه می کنیم. اگر کلید عنصر برابر با کلید گره ریشه باشد، عنصر را پیدا کرده ایم. در غیر این صورت، بسته به اینکه کلید عنصر کوچکتر یا بزرگتر از کلید گره ریشه باشد، به صورت بازگشتی زیر درخت چپ یا راست را جستجو می کنیم.

BSTها برای درج و حذف عناصر نیز کارآمد هستند. برای درج یک عنصر، ابتدا گره برگ را پیدا می کنیم که عنصر باید در آن درج شود. سپس با کلید عنصر یک گره جدید ایجاد می کنیم و آن را به عنوان فرزند گره برگ درج می کنیم. برای حذف یک عنصر، ابتدا گره حاوی عنصر را پیدا می کنیم. سپس به صورت بازگشتی گره را از درخت حذف می کنیم.

رایج ترین کاربردهای BST 

کاربرد درخت جستجوی دودویی

درخت‌های جستجوی دودویی (BST) یک ساختار داده بسیار متنوع هستند که می‌توانند برای کارهای مختلف استفاده شوند. برخی از رایج ترین کاربردهای BST ها عبارتند از:

• جستجو برای عناصر: BST ها یک ساختار داده بسیار کارآمد برای جستجوی عناصر هستند.

• میانگین پیچیدگی: زمانی برای جستجوی یک عنصر در یک BST O(log n) است ، جایی که n تعداد عناصر درخت است.

• درج عناصر : BST ها برای درج المان ها نیز کارآمد هستند. میانگین پیچیدگی زمانی برای درج یک عنصر در یک BST نیز O(log n) است.

• حذف عناصر : BST ها برای حذف عناصر نیز کارآمد هستند. میانگین پیچیدگی زمانی برای حذف یک عنصر در BST نیز O(log n) است.

• مرتب سازی عناصر: از BST ها می توان برای مرتب سازی عناصر در یک ترتیب جستجوی دودویی استفاده کرد. پیچیدگی زمانی برای مرتب‌سازی عناصر در یک BST O(n log n) است ، جایی که n تعداد عناصر درخت است.

• پیمایش: BST ها را می توان به روش های مختلفی از جمله به صورت سفارشی، پیش سفارش و پس از سفارش طی کرد.

علاوه بر این کاربردهای رایج، BST ها در کاربردهای مختلف دیگری نیز استفاده می شوند، مانند:

• سیستم های فایل: BST ها در سیستم های فایل برای ذخیره و سازماندهی فایل ها استفاده می شوند.

• کامپایلرها: BST ها در کامپایلرها برای پیاده سازی جداول نماد استفاده می شوند.

• پایگاه های داده : BST ها در پایگاه های داده برای پیاده سازی ایندکس ها استفاده می شوند.

• کدنویسی هافمن : BST ها در کدگذاری هافمن برای رمزگذاری داده ها استفاده می شوند.

• غلط گیر املا : BST ها در غلط گیر املا برای ذخیره و جستجوی کلمات استفاده می شوند.

BSTها یک ساختار داده قدرتمند هستند که می توانند برای کارهای مختلف استفاده شوند. آنها برای جستجو، درج و حذف عناصر کارآمد هستند و همچنین می توان از آنها برای مرتب کردن عناصر و عبور از درختان استفاده کرد. در نتیجه، BST ها یک ساختار داده محبوب در علوم کامپیوتر هستند و در بسیاری از برنامه های کاربردی مختلف استفاده می شوند.

BSTها یک ساختار داده قدرتمند هستند

نحوه درج یک عنصر در BST

برای درج یک عنصر در یک BST، مراحل زیر را دنبال می کنیم:

1. از گره ریشه شروع کنید.

2. عنصری که قرار است درج شود را با مقدار گره ریشه مقایسه کنید.

3. اگر عنصر کمتر از مقدار گره ریشه باشد، عنصر را به صورت بازگشتی در زیر درخت سمت چپ گره ریشه قرار می دهیم.

4. اگر عنصر بزرگتر از مقدار گره ریشه باشد، آنگاه عنصر را به صورت بازگشتی در زیر درخت سمت راست گره ریشه قرار می دهیم.

5. اگر عنصر برابر با مقدار گره ریشه باشد، هیچ کاری انجام نمی دهیم.

6. اگر گره ریشه یک گره برگ باشد، یک گره جدید با عنصر ایجاد می کنیم و آن را فرزند گره ریشه می کنیم.

درج یک عنصر در یک BST

مزایای درخت جستجوی دودویی

• جستجوی کارآمد: به طور متوسط، عملیات جستجو در یک BST متوازن دارای پیچیدگی زمانی O(log n) است که آنها را بسیار سریعتر از جستجوی خطی در آرایه‌ها یا لیست‌های پیوندی می‌کند.

• ساختار داده پویا: BST ها می توانند به راحتی با اضافه یا حذف عناصر بزرگ یا کوچک شوند.

• ذخیره سازی مرتب: داده ها به طور خودکار به ترتیب مرتب شده ذخیره می شوند و نیازی به مرتب سازی داده ها به طور جداگانه را از بین می برند.

• ساختار ساده: مفهوم اولیه درخت جستجوی دودویی نسبتاً ساده و قابل درک است.

مزایا و معایب درخت جستجوی دودویی

معایب درخت جستجوی دودویی

• درختان نامتعادل: اگر درخت جستجوی دودویی به دلیل ترتیب درج ضعیف نامتعادل شود، می‌تواند به فهرست پیوندی تنزل پیدا کند و باعث شود عملیات جستجو، درج و حذف ناکارآمد شود (O(n) در بدترین حالت پیچیدگی زمانی).

• عملکرد متغیر: کارایی درخت جستجوی دودویی به شدت به تعادل آن بستگی دارد. عملیات متعادل‌سازی می‌تواند به درج‌ها و حذف‌ها پیچیدگی اضافه کند.

• عملیات محدود: برخی از عملیات که در سایر ساختارهای داده کارآمد هستند (مانند جداول هش) ممکن است در درختان جستجوی باینری کارایی کمتری داشته باشند.

• پیاده‌سازی پیچیده: حفظ تعادل و مدیریت موارد مختلف لبه در درخت‌های جستجوی دودویی می‌تواند پیچیده باشد، به‌ویژه برای انواع خود متعادل کننده.

به طور خلاصه، درختان جستجوی دودویی ساختارهای داده با ارزشی هستند که در جداول جستجو، ذخیره سازی مرتب و نمادها کاربرد دارند. در حالی که آنها جستجوی کارآمد و مدیریت داده پویا را ارائه می دهند، عملکرد آنها می تواند تحت تأثیر مسائل تعادلی قرار گیرد.

درخت‌های جستجوی باینری متعادل، مانند درخت‌های AVL و درختان قرمز-مشکی، برخی از این کاستی‌ها را برطرف می‌کنند، اما پیچیدگی‌های خاص خود را دارند. انتخاب ساختار داده مناسب به کاربرد خاص و مبادلات مربوط بستگی دارد.

ویژگی درخت جستجوی دودویی

سوالات متداول درباره درخت جستجوی دودویی

1. BST چیست؟

BST یک ساختار داده درختی است که برای ذخیره و بازیابی داده ها استفاده می شود. BST ها به طور مرتب، مرتب می شوند، به این معنی که هر عنصر در BST بزرگتر از همه عناصر در سمت چپ آن و کوچکتر از همه عناصر در سمت راست آن است. این ویژگی درخت جستجوی دودویی را به یک ساختار داده بسیار کارآمد برای جستجوی داده ها تبدیل می کند.

2. درخت جستجوی دودویی چگونه کار می کند؟

برای جستجوی یک عنصر در یک BST، ابتدا به ریشه درخت می رویم. اگر عنصری که به دنبال آن هستیم برابر با مقدار ریشه باشد، کارمان تمام شده است. اگر عنصری که به دنبال آن هستیم کوچکتر از مقدار ریشه باشد، به زیردرخت چپ می رویم. اگر عنصری که به دنبال آن هستیم بزرگتر از مقدار ریشه باشد، به زیردرخت راست می رویم. این فرآیند را تا زمانی که عنصری که به دنبال آن هستیم را پیدا کنیم یا به یک برگ درخت برسیم ادامه می دهیم.

3. چگونه یک عنصر را در یک BST وارد کنیم؟

برای وارد کردن یک عنصر در یک BST، ابتدا باید محلی را برای آن در درخت پیدا کنیم. محلی که باید عنصر را در آن قرار دهیم جایی است که عنصر بزرگتر از همه اعداد در سمت چپ آن و کوچکتر از همه اعداد در سمت راست آن باشد. پس از پیدا کردن محلی برای عنصر، آن را در آن محل قرار می دهیم.

4. چگونه یک عنصر را از یک BST حذف کنیم؟

برای حذف یک عنصر از یک BST، ابتدا باید عنصری را که می خواهیم حذف کنیم پیدا کنیم. پس از پیدا کردن عنصر، باید پیوندهای آن را از درخت حذف کنیم. پیوندهایی که باید حذف شوند پیوندهای عنصر به فرزندان آن و پیوندهای فرزندان آن به عنصر هستند.

5. مزایای استفاده از BST چیست؟

BST ها ساختار داده ای بسیار کارآمد برای جستجوی داده ها هستند. آنها همچنین انعطاف پذیر هستند و می توان از آنها برای پیاده سازی مجموعه ها و جداول جستجوی پویا استفاده کرد.

6. معایب استفاده از BST چیست؟

BST ها می توانند پیچیده باشند و پیاده سازی آنها می تواند دشوار باشد. آنها همچنین می توانند فضای زیادی را اشغال کنند.

7.BST ها در کجا استفاده می شوند؟

BST ها در طیف گسترده ای از برنامه ها استفاده می شوند، از جمله:

- پایگاه داده ها

- رمزگذاری

- جستجوی متن

- مرتب سازی

سخن پایانی درباره درخت جستجوی دودویی

درخت جستجوی دودویی به عنوان یک ساختار داده مهم و کارآمد در علم کامپیوتر به‌طور گسترده‌ای مورد استفاده قرار می‌گیرد. این درخت با ویژگی‌های منحصربه‌فرد خود، امکان انجام عملیات جستجو، افزودن و حذف داده‌ها را با زمان‌های اجرا مناسب فراهم می‌کند.

درخت جستجوی دودویی به دلیل توانایی‌اش در مرتب‌سازی داده‌ها نیز در مواردی که نیاز به دسته‌بندی و مرتب‌سازی اطلاعات وجود دارد، بسیار مفید است. با این حال، برای دستیابی به عملکرد بهینه، لازم است درخت را به طور مناسب متعادل نگهداری کرده و به تعادل مناسب بین عملیات‌های درج و حذف توجه داشته باشیم.

گردآوری:بخش سرمایه های دیجیتال بیتوته